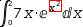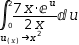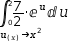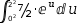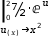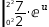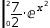4.4.3 U-Substitution with Definite Integrals
U-substitution can also be used with
definite integrals. The important point to note here is that the bounds of the integral
change as the integrator is rewritten. In
the path of transformations from integral to evaluation
there are two opportunities where this can
occur. The first opportunity is after u-substitution, when an integral
is decorated with a u-integrator. The second is after integration,
when the integrated expression is similarly decorated. In both of these cases,
selecting the decorator and applying U-Substitution remaps the bounds using the right side of the u-integrator. At the
same time, the decoration is removed and the expression is rewritten
in terms of the variable on the left side of the decoration.
Consider
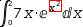 ∫0, 2, 7⋅x⋅ⅇ^.{x^2} ⅆx. Following u-substitution with
∫0, 2, 7⋅x⋅ⅇ^.{x^2} ⅆx. Following u-substitution with
 u=x^2, the integral is
u=x^2, the integral is
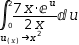 ∫0, 2, 7⋅x⋅ⅇ^u÷(2⋅x) ⅆ(u(x)→x^2).
∫0, 2, 7⋅x⋅ⅇ^u÷(2⋅x) ⅆ(u(x)→x^2).
After
simplifying, the
integral becomes
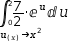 ∫0, 2, 7÷2⋅ⅇ^u ⅆ(u(x)→x^2).
∫0, 2, 7÷2⋅ⅇ^u ⅆ(u(x)→x^2).
(1)
Here is the first opportunity to remap the bounds. With the decorator
selected, apply
U-Substitution to produce an integral with remapped bounds.
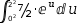 ∫0^2, 2^2, 7/2⋅ⅇ^u ⅆu.
∫0^2, 2^2, 7/2⋅ⅇ^u ⅆu.
Then proceed with integration and evaluation.
The second opportunity comes one step later. Starting with the
decorated integral in (1), integrate it to produce a decorated integration.
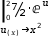 |0, 2, 7/2⋅ⅇ^u ⅆ(u(x)→x^2).
|0, 2, 7/2⋅ⅇ^u ⅆ(u(x)→x^2).
Select the decorator and apply
U-Substitution to produce a remapped integration with no decoration.
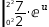 |0^2, 2^2, 7÷2⋅ⅇ^u ⅆu.
|0^2, 2^2, 7÷2⋅ⅇ^u ⅆu.
As before, proceed with evaluation.
If neither of the opportunities are taken, attempting to evaluate the decorated integrated
expression will result in the right side of the u-integrator being substituted
into the integrand to produce an unsubstituted integration
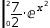 |0, 2, 7÷2⋅ⅇ^x^2 ⅆx.
|0, 2, 7÷2⋅ⅇ^x^2 ⅆx.